Tunis, 2,7 millions d’habitants, est située au sud de la Méditerranée. Sa forme et sa topographie sont propices à un champ thermique urbain complexe. Les mesures fixes et mobiles ont permis de mettre en évidence des paramètres de la variabilité spatiale de la température de l’air. En complément, la modélisation statistique et l’imagerie spatiale ont servi à estimer les valeurs dans des endroits dépourvus d’observations. Une situation nocturne a été simulée et validée par les températures de brillance issues d’une image satellitaire ASTER-TIR. Le coefficient de détermination du modèle statistique atteint 0,9 la nuit par temps calme.
Mapping temperatures in Tunis using statistical modelization and teledetection
Tunis, with a population of 2.7 million, is located south of the Mediterranean Sea. Its topography and shape impacts its urban thermal field. Meteorological records given by network stations and mobile surveys have highlighted a multitude of parameters that explain the spatial variability of air temperature. In addition, modelling and satellite images were used to estimate the values in areas without observations. Night-time situations were simulated and validated by brightness temperatures given by satellite image. The determination coefficient of the statistical model reaches 0.9 at night.
Key words : modelling, remote sensing, temperature, Tunis
Cartografía de las temperaturas en Túnez mediante modelización estadística y teledetección
Túnez, con 2,7 millones de habitantes, se sitúa al sur del Mediterráneo. Su forma y topografía propician un complejo espacio térmico. Las mediciones en puntos fijos y móviles han permitido identificar los parámetros de variabilidad espacial de la temperatura del aire. Complementariamente, mediante modelización estadística e imágenes digitales se han podido estimar los espacios sin observaciones. Los valores nocturnos se han simulado y validado por los resultados de temperatura efectiva ofrecidos por la imagen del satélite ASTER-TIR. En noches sin gran variabilida, el coeficiente de determinación del modelo estadístico puede alcanzar el 0.9.
Palabras clave : modelización, sensores remotos, temperaturas, Túnez
Introduction
L’îlot de chaleur urbain (ICU) est défini comme l’écart thermique entre la partie dense d’une agglomération et sa périphérie rurale (Oke, 1981). C’est un phénomène de beau temps qui apparaît principalement en phase nocturne (Cantat, 2004). Cependant, durant la journée, la ville peut être plus fraîche que la campagne, dans les zones semi-arides (Rasul et al., 2015 ; Lazzarini et al., 2013). La croissance des villes a généré des climats artificiels, développant fréquemment certains problèmes liés au phénomène de l’ICU, comme les pics de pollution et la surconsommation énergétique induite par la climatisation électrique (Vinet, 2000).
La gestion d’éventuels aléas, comme les canicules, exige la compréhension de la variabilité spatio-temporelle de la température à l’échelle urbaine. Cette dernière n’est pas une simple manifestation d’un phénomène commandé à l’échelle régionale ou planétaire. Elle obéit principalement à des logiques spatiales d’échelles beaucoup plus fines. Parfois, il suffit d’un faible déplacement pour constater de fortes variations thermiques (Carrega, 2003). Toutefois, les différents types de mesures de la température de l’air (à 2 m de la surface) restent ponctuels dans le temps et dans l’espace. Pour remédier à ce problème, plusieurs études récentes recourent à la modélisation. Cette technique permet d’améliorer les prévisions météorologiques et de mieux comprendre le climat à l’échelle urbaine (Kusaka, Kimura, 2004).
La modélisation est très développée dans le domaine de la prévision météorologique. Ainsi, plusieurs modèles ont été développés tels que GFS, UKMO, RAMS, MM5, BOLAM. En climatologie, plusieurs études ont été réalisées à différentes échelles spatio-temporelles, entre autres la modélisation des pluies (Laborde, Traboulsi, 2002 ; Obled, 1987 ; Creutin et al., 1980), des concentrations des polluants (Martin, 2008 ; Dahech, 2007 ; Pielke et al., 1987), des ambiances bioclimatiques (Segal, 1981) et des températures (Joly et al., 2009 ; Atkinson, 2003 ; Dodson et Marks, 1997 ; Fury, Joly, 1995 ; Willmott, Matsura, 1995 ; Carrega, 1994 ; Oke et al., 1991). Les méthodes de modélisation sont très nombreuses, se regroupant en trois approches : statistique, fondée sur les mesures de terrain, physique, qui utilise les équations du bilan d’énergie, et numérique dynamique, qui introduit la composante advective du climat (Atkinson, 2003). L’approche statistique présente l’avantage d’être facile à appliquer et de s’appuyer sur des mesures de terrain plus fiables que les lois physiques prédéfinies. Le principe consiste, selon une démarche inductive, à se baser sur les températures mesurées ponctuellement dans un espace donné, pour estimer, avec le moins d’erreurs possible, les données manquantes pour chaque nœud ou chaque centre de carreau élémentaire d’une maille régulière (Carrega, 1994).
Théoriquement, la température de l’air en ville se répartit en auréoles concentriques de valeurs décroissantes du centre vers la périphérie. Mais ce champ thermique se complique singulièrement lorsque le site de la ville juxtapose des plans d’eau, collines, plaines, dépressions et djebels, comme c’est le cas à Tunis. Les expérimentations au niveau de cette métropole, par le biais des mesures itinérantes, ont permis de mettre en évidence des paramètres liés aux caractéristiques urbaines du site (les canyons, les parois, l’orientation des rues…) et liés au cadre naturel (sebkha1, espace vert, éloignement de la mer). L’objectif du présent travail est d’abord de simuler le champ thermique nocturne de l’agglomération de Tunis, selon une démarche inductive qui consiste à établir « un modèle fonctionnel » à partir des lois qui relient les températures aux paramètres caractéristiques des sites de mesure. Ensuite, la fiabilité du modèle a été vérifiée à partir de la méthode de rééchantillonnage Bootstrap. La sortie du modèle a été enfin croisée aux températures de brillance issues d’une image ASTER-TIR (Advanced Spaceborne Thermal Emission and Reflection Radiometer/Thermal Infrared Radiometer).
Zone d’étude
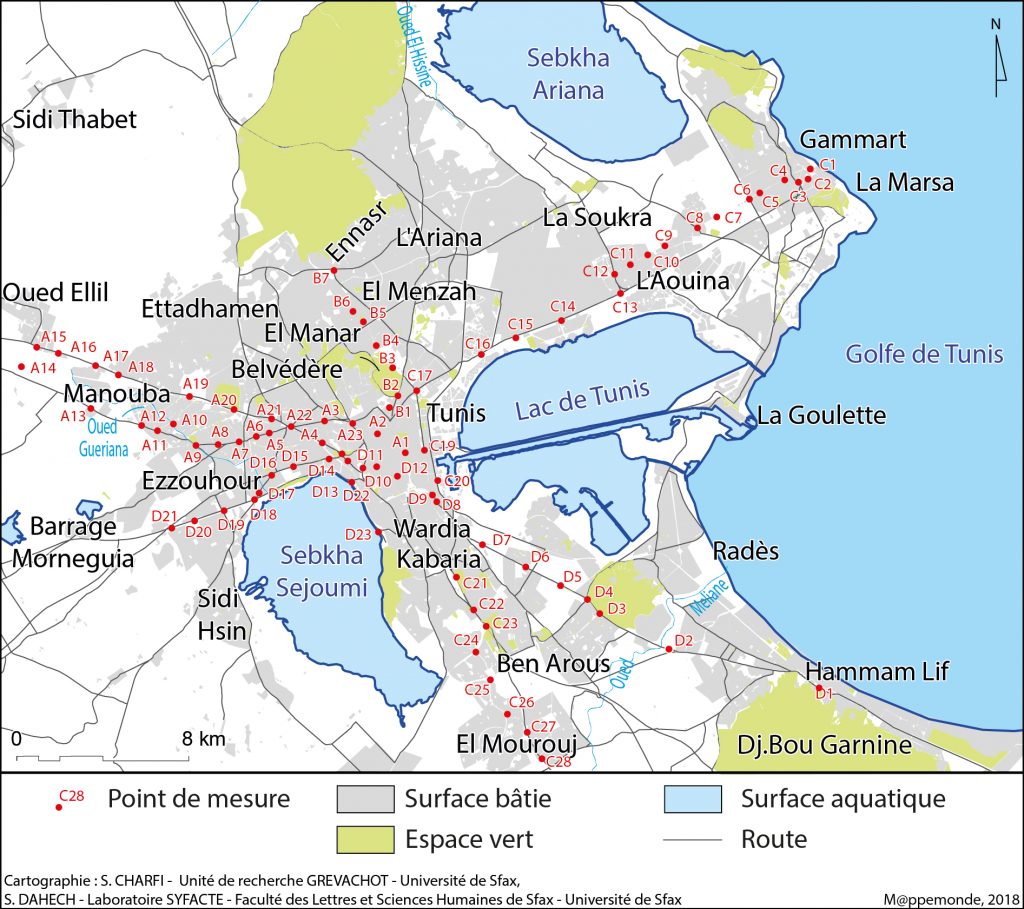
L’agglomération de Tunis est située au fond d’un golfe, au bord de la Méditerranée. Elle occupe une plaine côtière basse, parsemée de collines molles et allongées, orientées souvent NNW-SSE. Elle est marquée par sa forme caractéristique en éventail resserré au niveau de son centre par deux surfaces aquatiques : Sabket Sijoumi et le lac de Tunis (figure 1). Il s’agit d’un milieu fortement anthropisé qui abrite près de 2,7 millions d’habitants en 2014. L’appellation « Tunis » s’applique communément à toute l’agglomération composée de 4 gouvernorats : Tunis, Ariana, Ben Arous et Manouba. Ce cadre cerne des traits climatiques particuliers, grâce à une multitude de facteurs qui agissent à différentes échelles: régionale et locale. Ces éléments pourraient être des facteurs de discrimination thermique en milieu urbain.
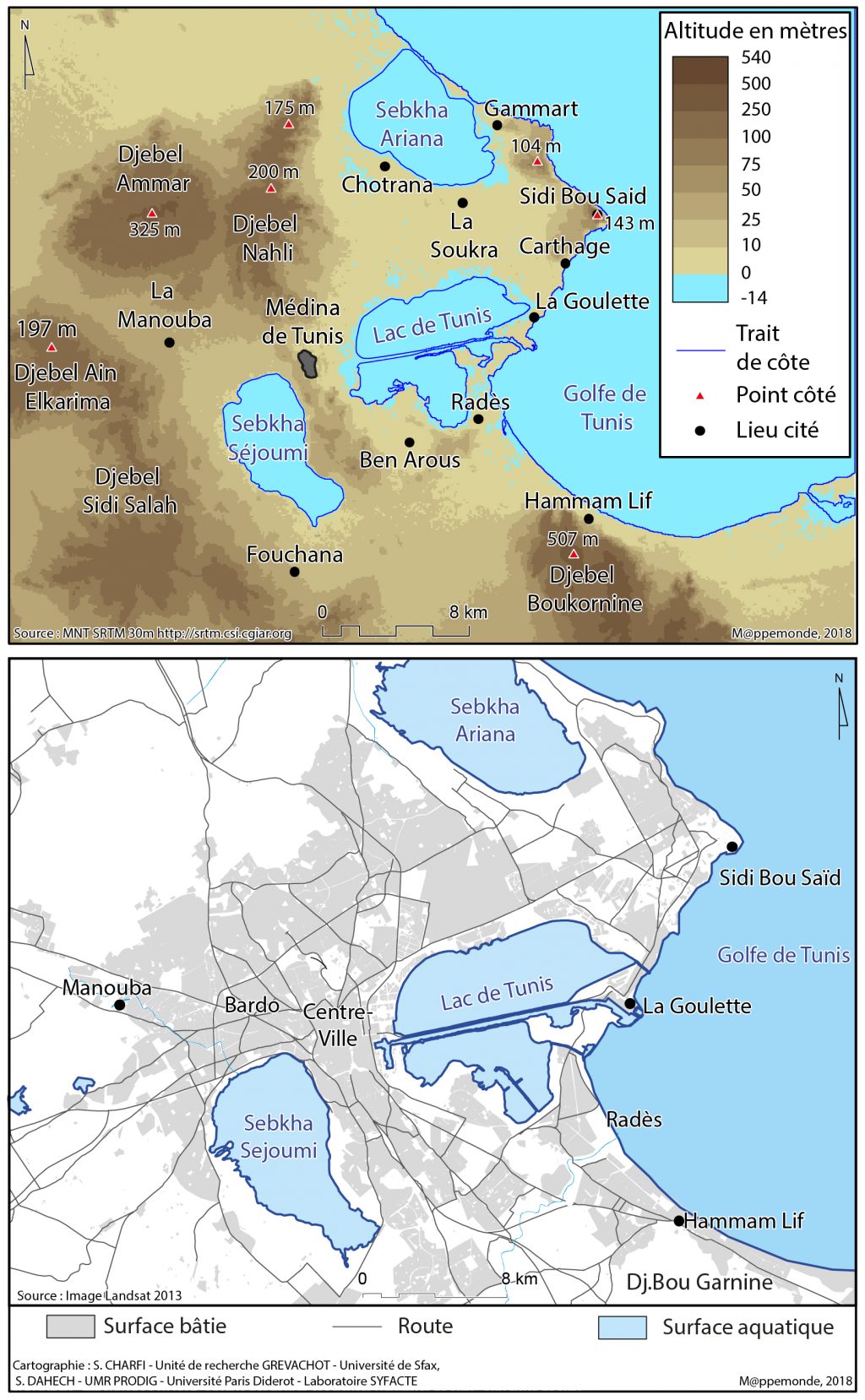
Figure 1. Localisation et cadre géographique : tissu urbain (en haut) et topographie de l’agglomération de Tunis (en bas).
Méthodes et données
Modélisation
L’approche retenue consiste à établir « un modèle fonctionnel » à partir des lois qui relient les températures dans l’agglomération de Tunis aux paramètres caractéristiques des sites de mesure. D’après la littérature (Kljun et al., 2004 ; Schmid, 2002 ; Schmid, 1994), la température observée à un point donné est conditionnée par des caractéristiques d’une zone plus large. Il s’agit de plusieurs facteurs microclimatiques et locaux de natures diverses dont l’effet est variable d’un jour à l’autre et d’une saison à une autre. Plusieurs études (Brandsma, Wolters, 2012 ; Charfi, 2012 ; Bridier, 2009 ; Joly et al., 2009 ; Kuttler et al., 1996 ; Fury, Joly, 1995, 1998 ; Carrega, 1994 ; Oke, 1988, 1981) ont prouvé que la modélisation statistique peut fournir des informations quantitatives utiles sur la variabilité spatio-temporelle de la température en utilisant différents paramètres naturels et/ou liés à la ville. Nous avons adopté la méthode développée par Carrega (1994) qui a approché ces paramètres par le biais des éléments morphométriques, à savoir la distance au mur (effet de paroi), la distance au centre-ville (ratio espace bâti/espace libre), l’aération et la densité du bâti. En outre, il a détaillé les effets géographiques tels que la distribution du relief (exposition, pente, la position aval, l’orientation…), les types d’occupation du sol, l’éloignement de la côte… Les différents facteurs, tous types confondus, font varier spatialement la température selon un emboîtement hiérarchique d’échelles, du niveau régional (latitude, longitude, continentalité…) jusqu’au niveau local (altitude, pente, orientation, distance du centre…) et microclimatique (aération, type de substrat…).
Dans le présent travail, les structures qui commandent la température dans la situation modélisée sont définies à partir des points de mesures nocturnes réalisées dans la zone d’étude. C’est pour cette raison qu’il nous a semblé important de caractériser le cadre naturel et urbanistique autour des points de mesure allant de quelques dizaines de mètres (pour les variables qui agissent à micro-échelle) à quelques centaines ou milliers de mètres (échelle locale). Les enregistrements thermiques ont été réalisés le long de 6 transects et contiennent 62 points de mesures choisis de façon qu’ils couvrent une grande partie de l’agglomération et qu’ils soient représentatifs de la variété du tissu urbain et de la topographie (figure 2). Les mesures, réalisées la nuit, se sont déroulées en voiture roulant à une vitesse constante de 50 km/h, de façon que les sondes thermiques soient ventilées. Nous avons essayé aussi d’éviter les embouteillages et leurs effets perturbateurs. Pour cette raison, nous avons choisi des points facilement accessibles en voiture. Il est important de signaler aussi que la durée de la campagne est d’environ 40 mn. Le but était que la variation de la température mesurée entre les points de chaque itinéraire soit due à une variation spatiale, et non à une variation temporelle, ce qui constitue par définition l’objectif de ce genre de mesures (Erpicum, 1989 ; Carrega, 1994 ; Garcia, Carrega,1998 ; Charfi, 2012).
Deux principes ont constamment guidé le choix des variables sélectionnées pour le modèle : d’abord le recours à la littérature (Lindberg, 2007 ; Bottyán, Unger, 2003 ; Joly et al., 2003 ; Miller, 2002 ; Carrega, 1994 ; Hocking, 1976) et ensuite la bonne connaissance des particularités naturelles de l’agglomération de Tunis. Pour cette raison, nous avons adopté une stratégie fondée sur le principe de la construction d’un jeu de variables géographiques classées suivant leur corrélation avec les températures. Enfin, le modèle fonctionnel a été construit à partir des régressions multiples pas à pas, prenant en compte le rôle des descripteurs statistiquement significatifs attestés par la méthode de Bootstrap (Efron, Tibshirani, 1993 ; Efron, 1979). Il s’agit d’une forme de rééchantillonnage permettant l’estimation des limites de confiance d’un modèle de régression linéaire (Palm, 2002).
L’équation recueillie a été traitée dans un système d’information géographique sous IDRISI, moyennant l’outil mapping calculator, pour reconstituer le champ thermique avec une grille de 1 323 colonnes et de 1 317 lignes centrée sur l’agglomération de Tunis, suivant une résolution de 90 m, soit la même que l’image satellitaire utilisée dans ce travail.
Les paramètres qui pourraient expliquer la variabilité spatiale de la température sont de deux types :
- géographiques, liés au site et au cadre naturel : distance à la mer, pente, altitude et exposition, végétation ;
- anthropiques, liés à la ville : distance au centre-ville, distance au parois, largeur des rues, taux de la surface bâtie.
Ils sont de deux sources différentes :
- un modèle numérique de terrain (MNT), qui provient du serveur de données de la NASA, Global Land Cover Facility (GLCF) (Jarvis et al., 2008), disponible à l’adresse http://srtm.csi.cgiar.org. Il propose des données RADAR obtenues par interférométrie, lors de la mission SRTM (Shuttle Radar Topography Mission), avec une précision horizontale de 90 m et verticale de 1 m. Selon Bridier (2009), la meilleure résolution n’est pas la plus fine, car l’excès de précision est nuisible, à la fois à cause de la masse de données à traiter, et à cause du brouillage induit par le détail. Une précision horizontale de 50 m est généralement suffisante pour l’ensemble d’une ville ou d’une agglomération. Le MNT représente l’ensemble des données relatives au relief. Il est constitué de fichiers comportant les coordonnées : longitude (X), latitude (Y) et altitude (Z) attribuées à chaque maille de la grille. Ces fichiers ont été d’abord mis en forme puis traités avec les outils disponibles sur IDRISI pour extraire la pente et l’orientation. Ces deux paramètres traduisent le degré d’exposition au rayonnement solaire pendant la journée et donc déterminent les secteurs qui reçoivent le plus d’énergie ;
- l’Indice de Végétation Normalisée (NDVI) et la densité du bâti qui ont été calculés à partir d’une image Landsat TM diurne. Elle date du 2 août 2013 avec une résolution spatiale de 28 m, prise par type de temps radiatif. Les cartes produites (NDVI et bâti) et le modèle numérique de terrain ont été intégrés dans un système d’information géographique (SIG).
Les paramètres mentionnés dans l’équation du modèle sont faciles à déduire, d’une part, et sont les éléments significativement corrélés, d’autre part.
Image satellite
Pour étudier la variabilité spatiale de la température de surface, nous avons utilisé une scène ASTER-TIR. Le capteur Advanced Space borne Thermal Emission and Reflection Radiometer/Thermal Infrared Radiometer embarqué à bord du satellite Terra de la NASA offre la possibilité de caractériser la température de surface nocturne à une échelle spatiale relativement fine. Nous disposons d’une scène Aster de 90 m de résolution, prise par temps radiatif, le 31 octobre 2005 à 21h26mn TU. L’ASTER-TIR est doté de 5 canaux dans l’infrarouge thermique. Pour en extraire la température de surface, nous avons utilisé la méthode Multi-Channel Sea-Surface Température (MCSST) développée par Matsunaga (1996).
L’image satellitaire citée ci-dessus a été corrigée géométriquement suivant le système de projection UTM Carthage avant d’être soumise à une classification non supervisée. Les résultats sont intégrés dans un Système d’Information Géographique permettant la superposition des données afin de faciliter l’approche comparative.
Simulation du champ thermique nocturne de l’agglomération de Tunis
Grâce à un réseau très dense constitué de 62 points de mesure assez bien répartis dans l’espace, un modèle statistique a été établi donnant des résultats satisfaisants.
Tn = 25,4 – 0,0001*distance/mer – 0,0001*distance/centre + 0,024*% bâti – 3,6*NDVI
l’écart absolu moyen des résidus 0,7, moyenne des écarts de T : 2,3°C
Le coefficient de détermination atteint 0,94 et l’écart-type des résidus est relativement faible (0,84°C) par rapport à celui de l’échantillon (3,5°C). L’estimation des limites de confiance du modèle par méthode du Bootstrap confirme la fiabilité du modèle bien que la valeur de la pente « a » relative à la variable « distante au centre » dépasse la borne supérieure de l’intervalle de confiance « Bca ». Cela s’explique par le poids relativement faible de ce paramètre dans le modèle.
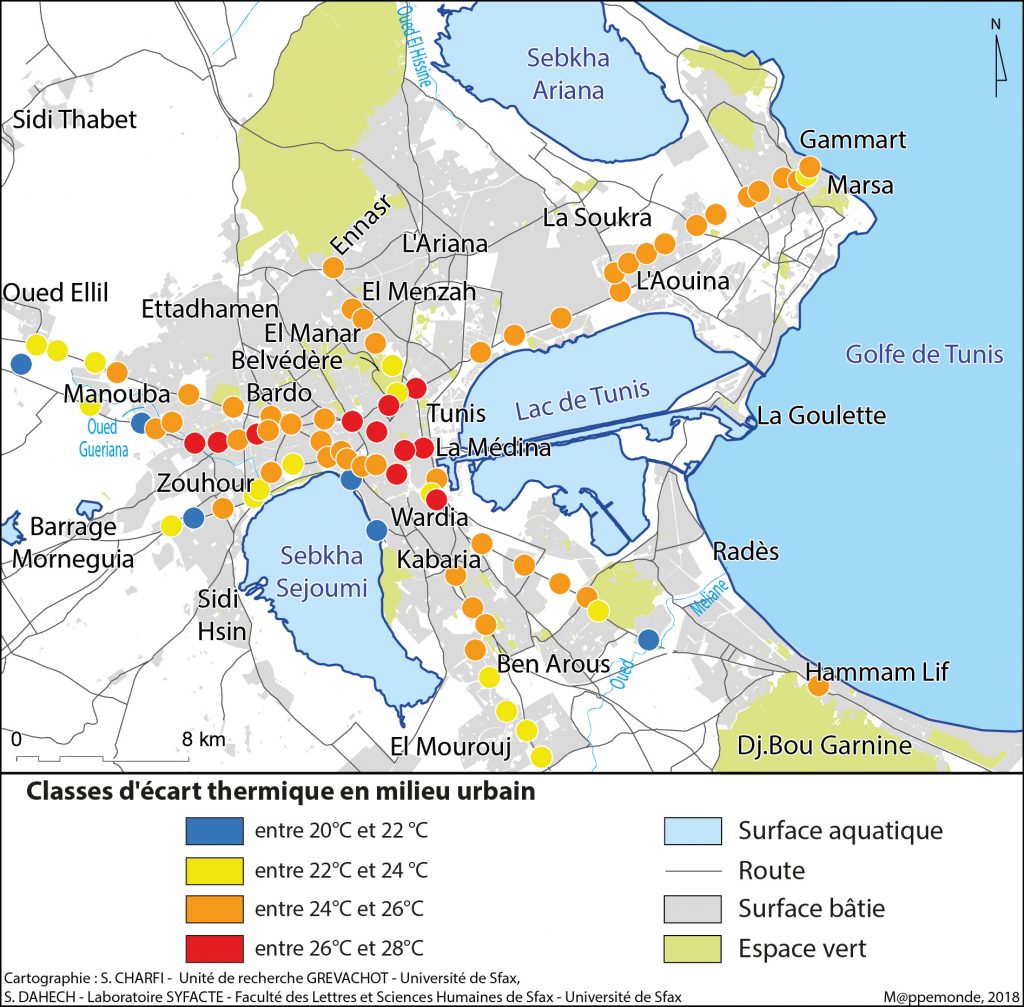
La densité du réseau de mesure fait apparaître l’effet de la mer comme un facteur déterminant dans le modèle : en effet, la température baisse au fur et à mesure que la distance à la mer augmente la nuit en été, passant de 28°C sur la côte (le cas à la Marsa, Hammam Lif et Rades) à 23°C au niveau des zones rurales situées à l’ouest (le cas à Sidi Thabet) (figures 3, 4). Cependant, elle croît avec la densité du bâti ; en effet, la sortie du modèle montre que les zones densément urbanisées sont les plus chaudes comme c’est le cas dans la partie centrale de l’agglomération et les quartiers les plus denses au nord-ouest (Ettadhamen) et au sud (Ben Arous). La distance au centre est négativement corrélée à la température expliquée par l’effet de l’îlot de chaleur urbain. À ce propos, la baisse de la température s’effectue d’une manière plus ou moins brutale du centre (médina) vers la périphérie ouest (Manouba, Morneguia…), fortement végétalisée et à topographie basse favorable à l’accumulation de l’air froid. Dans le même ordre d’idées, la densité de la biomasse végétale, exprimée dans le modèle par l’indice NDVI, s’avère inversement proportionnelle à la température. Pendant la saison sèche, la faiblesse de la réserve hydrique dans le sol amplifie le poids des surfaces végétalisées, plus humides. Plus la végétation est dense, plus la température baisse. C’est pour cette raison que les espaces végétalisés se transforment la nuit en cellules froides comme c’est le cas du parc du Belvédère, du centre sportif El Menzeh, de l’aéroport de Tunis-Carthage…
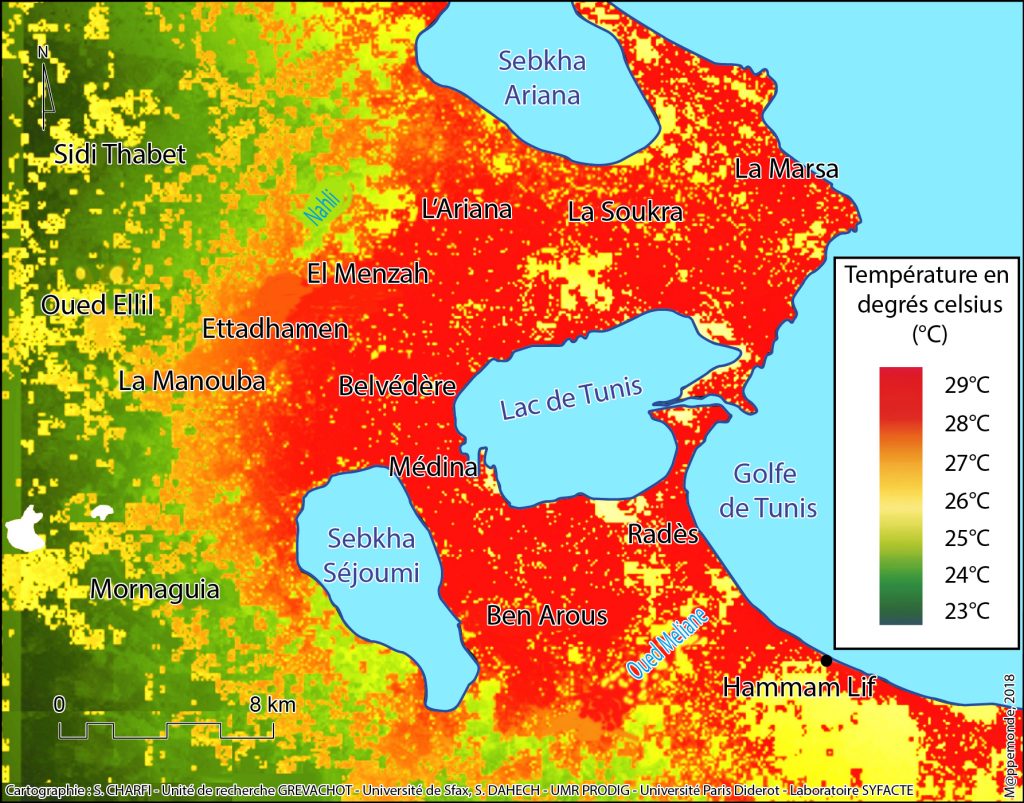
Figure 4. Simulation du champ thermique nocturne de l’agglomération de Tunis: Cas du 28/8/2007 à 1h50mn TU.
Au terme de cette analyse, plusieurs conclusions ont pu être dégagées.
Le phénomène de l’îlot de chaleur urbain a été mis en évidence par temps calme et ciel dégagé, traduit par la décroissance de la température avec l’éloignement du centre le plus densément urbanisé, de 0,2°C/km. Le modèle sélectionné a permis de se rendre compte de la significativité importante de la distance à la mer et des zones végétalisées qui se transforment en cellules froides. La température baisse de 0,2°C lorsque l’on s’éloigne de 1 km de la côte et de 2 à 3°C au niveau des espaces verts. Une variable à ne pas négliger est la densité du bâti qui est positivement corrélée à la température, soit 0,1°C à 0,3°C pour 10% du bâti. La comparaison des paramètres de simulation des températures nocturnes montre un poids comparable pour les facteurs liés à la ville et ceux liés au cadre naturel.
Spatialisation du champ thermique de surface de l’agglomération de Tunis à partir de l’image ASTER-TIR
Il est nécessaire d’insister au début sur le décalage de deux mois entre cette image (figure 5) et la simulation de comparaison (28 août) bien qu’il s’agisse de types de temps radiatifs. C’est pourquoi nous avons choisi de travailler sur les écarts thermiques par rapport à la référence urbaine et non sur les températures absolues.
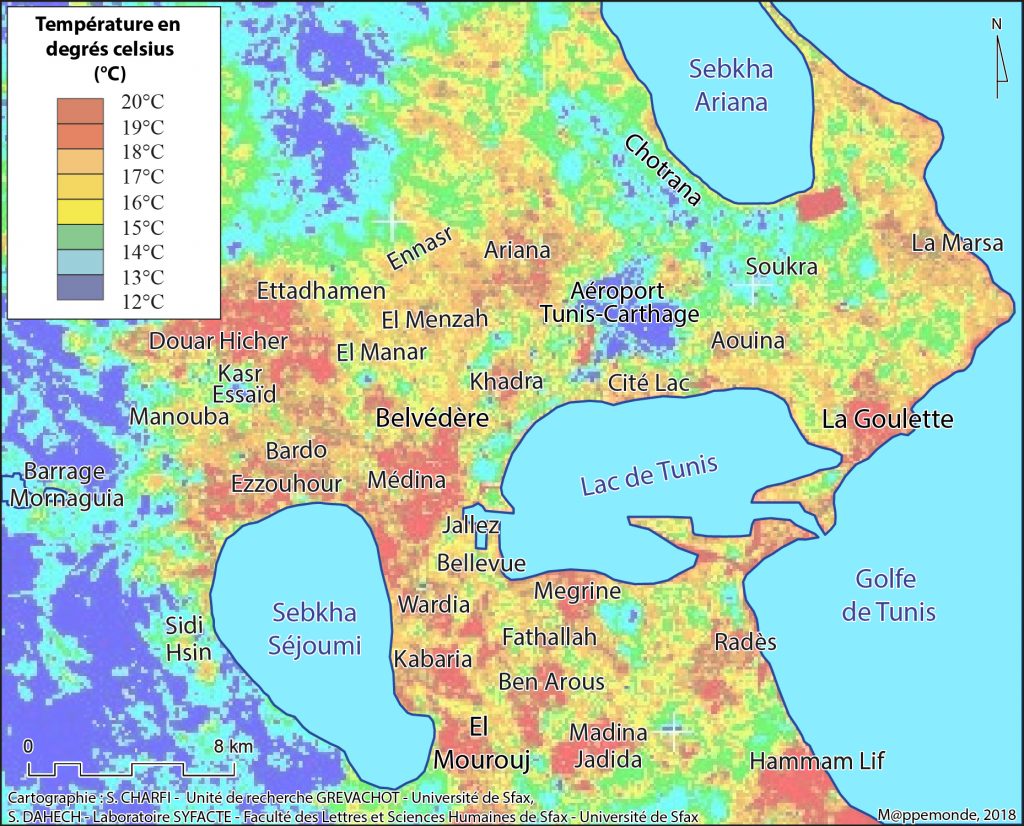
Figure 5. Champ thermique de surface nocturne dans la zone centrale de l’agglomération de Tunis par temps radiatif à partir d’une scène ASTER TIR datée du 31/10/2005 à 21h26 TU.
La résolution relativement fine de l’image ASTER TIR (90 m) laisse voir plusieurs détails (Liu, Zhang, 2011 ; Song, Park, 2014) : les températures de surface montrent une variation de l’ordre de 12 à 20°C et donc une amplitude thermique d’environ 8°C, comparable à celle prédite par le modèle (7,6°C). À l’échelle de la zone agglomérée apparaît une forte hétérogénéité thermique : au centre-ville, certaines surfaces fraîches correspondent aux reliefs les plus élevés non urbanisés tels que Jallaz, Bellevue, Karrouba et Fathallah et à des espaces verts tel le parc urbain du Belvédère. Le noyau chaud central apparaît non compact avec une cellule chaude principale au niveau de la Médina et d’autres plus petites au niveau des quartiers les plus proches tels que Omrane et Khadra au nord, Saïda Mannoubia, Wardia, Lacagna, Kabaria et Ben Arous au sud.
Plus loin, vers le nord et l’ouest, un archipel d’îlots de fraîcheur correspond aux lieux fortement végétalisés tels que les complexes sportifs (El Menzeh et Kasr Saïd) et aux terrains non bâtis comme l’aéroport de Tunis-Carthage. Ils sont également très nets sur la sortie du modèle avec une baisse d’environ 2°C. Cependant, de forts micro-îlots de chaleur sont mis en évidence dans les secteurs les plus fortement urbanisés tels les quartiers populaires de Ettadhamen et Douar Hicher au nord-ouest, le centre-ville d’Ariana au nord, les quartiers de Zouhour au sud-ouest et de Madina Jadida et El Mourouj au sud. À ce niveau, de très nettes différences de la thermographie de surface entre l’habitat pavillonnaire d’une part et l’habitat populaire d’autre part sont observées. En effet, des îlots, où la chaleur est relativement moins intense, regroupent les quartiers résidentiels à habitat pavillonnaire, telles les cités Manar, El Menzeh, Ennasr, au nord, et Manouba, à l’ouest. Ce gradient, qui peut atteindre 4°C dans les quartiers populaires, s’explique vraisemblablement par la couleur sombre des toitures très mal entretenues, leur tissu très serré et la rareté des zones industrielles dont les constructions, généralement de type métallique, paraissent relativement fraîches comme c’est le cas de Kasr Saïd. Ce type de matériaux peu inerte favorise une déperdition calorifique rapide dès le coucher du soleil et donc se refroidit vite. En outre, le tissu urbain des zones industrielles est moins dense et la végétation plus abondante. À la périphérie de l’agglomération, sur la carte simulée comme sur l’image satellite, les zones fraîches sont mieux individualisées et plus homogènes. Elles correspondent à des paysages plus ou moins ruraux. Elles sont constituées de terrains agricoles tels que ceux de la vallée de l’oued Miliane au sud, la cuvette de Manouba à l’ouest, la plaine de Chotrana au nord-est et le parc urbain Nahli au nord-ouest.
En somme, le recoupement des écarts de température de brillance par rapport à la référence urbaine avec ceux estimés par le modèle montre une très forte corrélation (figure 6).
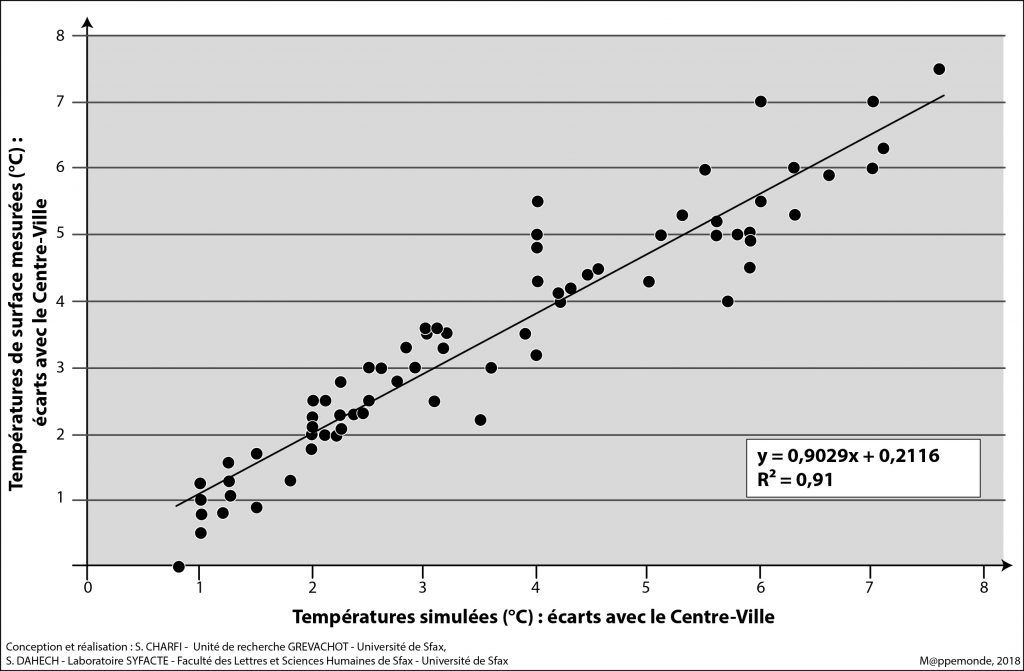
Figure 6. Croisement des écarts thermiques par rapport au point de référence urbaine des valeurs prédites par le modèle (28-08-2007) et celles qui leur correspondent sur l’image Aster (31-10-2005).
En effet, la droite de régression résume 91% du nuage de points. Le modèle est performant la nuit en raison de la forte corrélation entre la température de surface et celle de l’air d’une part, et d’autre part, à cause des facteurs déterminants de la température de l’air en phase nocturne par temps calme. En effet, en l’absence d’advection, la température de l’air durant les nuits calmes dépend en grande partie de la nature de la surface et de ses caractéristiques physiques.
Par souci de clarté, nous avons dressé un schéma de comparaison entre les mesures du rayonnement thermique émis dans le domaine de l’infrarouge par les surfaces diverses à partir de l’image Aster et celles de l’air mesurées le 28-08-2007. Le but ici est double : d’une part, montrer la répartition des températures dans la ville et, d’autre part, montrer à quel point la température de surface pourrait influencer celle de l’air qui la recouvre. Onze sites différents de mesures ont été sélectionnés sur un axe routier allant de La Marsa, à l’est, vers la cité Zouhour, à l’ouest. L’examen des courbes d’évolution du gradient thermique par rapport à la référence urbaine montre une forte concordance entre les variations de la température de surface et celles de l’air qui la recouvre. En effet, l’air est de plus en plus chaud au fur et à mesure que la surface sous-jacente est chaude (figure 7).
Toutefois la température de l’air s’avère moins sensible aux changements de sites. L’écart thermique par rapport à la référence urbaine est en moyenne plus marqué en surface que dans l’air sur tout l’itinéraire (1,9°C) avec un maximum au niveau des surfaces végétalisées (2,8°C). Les températures de surface sont plus variées que celles de l’air en raison de la complexité des types de couvertures du sol en milieu urbain et des variations de la morphologie urbaine (Xian, 2015). En outre, le substrat, constitué surtout d’asphalte et de béton, a une forte capacité de réchauffement à cause de sa nature et de sa couleur foncée (cp de l’asphalte = 1021 J·kg−1·K−1. Cependant, l’air répond moins aux fluctuations de température à cause de sa forte chaleur massique : cp de l’air = 1004 J/(kg·K).
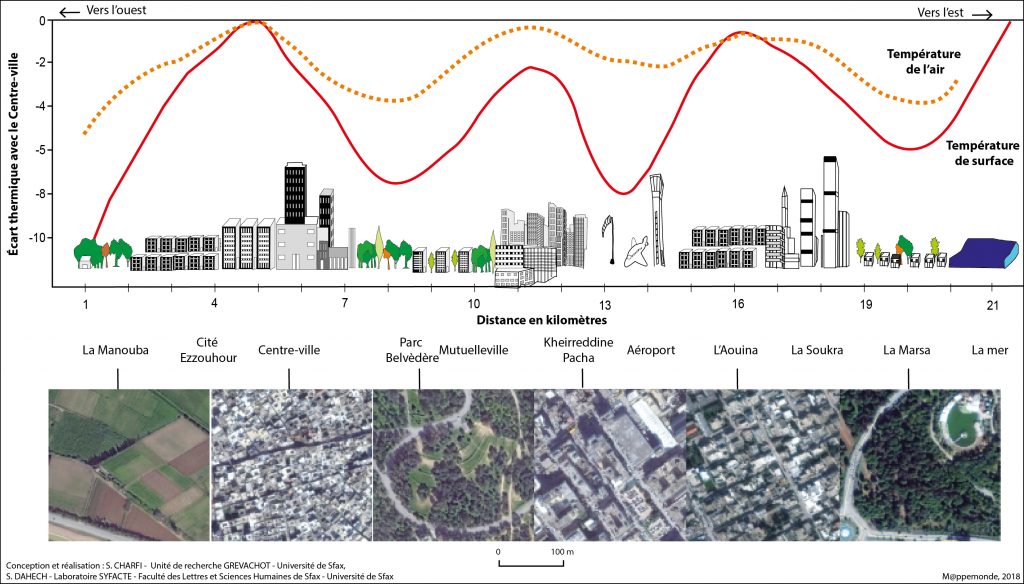
Figure 7. Croisement des écarts thermiques au point de référence urbain des températures de l’air (à 2m) et de surfaces issues de l’image Aster (31-10-2005).
Conclusion
La simulation réalisée à partir d’un modèle statistique a permis d’estimer les valeurs de température là où il n’y avait pas de mesures. Le passage des mesures ponctuelles à la simulation a apporté des informations supplémentaires sur l’agencement spatial des températures à l’échelle de l’agglomération, mais avec une perte parfois très sensible en matière de fiabilité et de précision. Les relations souvent complexes, qui gèrent les variations de la température surtout à l’échelle de la zone urbaine, peuvent laisser parfois une grande partie de l’information inexpliquée.
L’analyse du champ thermique de surface à l’échelle de l’agglomération confirme les disparités spatiales de la température de brillance la nuit et la présence d’îlots de chaleur intense comparable à celle enregistrée dans l’air à 2 m du sol. Le croisement des écarts thermiques aux points de référence urbains prédits par le modèle avec ceux à la surface a permis de relever la bonne performance du modèle d’estimation de la température de l’air la nuit en raison de l’absence du rayonnement direct et de la faiblesse des advections.
Bibliographie
Atkinson B.W. (2003). « Numerical modelling of urban heat island intensity ». Boundary-Layer Meteorology, vol. 109, p. 285-310.
Bottyan Z., Unger J. (2003). « A multiple linear statistical model for estimating the mean maximum urban heat island ». Theoretical And Applied Climatology, vol. 75, p. 233–243.
Brandsma T., Wolters D. (2012). « Measurement and Statistical Modeling of the Urban heat Island of the City of Utrecht (the Netherlands) ». Journal of Applied Meteorology and Climatology, vol. 51, n°6, p. 1046-1060.
Bridier S. (2009). « Variabilité spatio-temporelle des brises thermiques en milieu urbain selon l’analyse morphométrique du relief et l’analyse de l’occupation du sol ». Journées de climatologie, Besançon, p. 51-60.
Cantat O. (2004). « L’îlot de chaleur urbain parisien selon les types de temps ». Norois, n°191/2, p. 75-102.
Carrega P. (1994). « Topoclimatologie et Habitat ». Thèse, Revue de géographie du laboratoire d’analyse spatiale Raoul Blanchard, n°35 et 36, Université de Nice, France, 408 p.
Carrega P. (2003). « Le climat aux échelles fines ». Publication de l’Association internationale de climatologie, vol. 15, p. 19-30.
Charfi S. (2012). « Le comportement spatio-temporel de la température dans l’agglomération de Tunis ». Thèse de doctorat de l’Université de Tunis et de l’Université de Nice, 311 p.
Creutin D., Obled C., Tourasse P. (1980). « Analyses spatiale et temporelle des épisodes pluvieux cévenols ». La Météorologie, vol. 6, n°20-21, p. 233-242.
Dahech S. (2007). « Le vent à Sfax (Tunisie), impacts sur le climat et la pollution atmosphérique ». Thèse de doctorat de l’Université Paris 7, 309 p. + annexes.
Dodson R., Marks D. (1997). « Daily air temperature interpolated at high spatial resolution over a large mountainous region ». Climate research, vol. 8, p. 1-22.
Efron B., Tibshirani R.J. (1993). « An Introduction to the Bootstrap ». New York : Chapman and Hall, p. 436.
Efron B. (1979). « Bootstrap methods : another look at the jackknife ». The Annals of Statistics, vol. 7, n°1, p. 1-26.
Erpicum M. (1989). « Analyse de la variabilité spatiale de la température à l’aide de transects mobiles (application en topoclimatologie)» . Publications de l’Association internationale de climatologie, vol. 2, p. 63-67.
Fury R., Joly D. (1995). « Interpolation spatiale à la maille fine des températures journalières ». La Météorologie, vol. 8, n°11, p. 36-43.
Garcia E., Carrega P. (1998). « Aspects de la climatologie urbaine de la ville de Marseille à travers des mesures itinérantes ». Publications de l’Association internationale de climatologie, vol. 11, p. 424-432.
Hocking R.R. (1976). « The analysis and selection of variables in linear regression ». Biometrics, vol. 32, n°1, p. 1-49.
Jarvis A., H.I. Reuter, A. Nelson, E. Guevara (2008). Hole-filled seamless SRTM data V4. International Centre for Tropical Agriculture (CIAT).
Joly D. et al. (2003). « Temperature interpolation at a large scale ; test on a small area in Svalbard ». International Journal of Climatology, vol. 23, n°13, p. 1637-1654.
Joly D., Fury R. (1998). « Méthode d’interpolation des températures à échelle fine mise en évidence des zones d’interpolation critique ». Publications de l’Association internationale de climatologie, vol. 11, p. 265-275.
Joly D., Bois B., Zaksek K. (2009). « Hiérarchie des facteurs topographiques qui commandent la variation spatiale des températures ». Journées de climatologie, Besançon, p. 15-34.
Kljun N. et al., (2004). « A simple parameterisation for flux footprint predictions ». Boundary-Layer Meteorology, vol. 112, n°3, p. 503-523.
Kusaka H., Kimura F. (2004). « Coupling a Single-Layer Urban Canopy Model with a Simple Atmospheric Model : Impact on Urban Heat Island Simulation for an Idealized Case ». Journal of the Meteorological Society of Japan, vol. 82, n°1, p. 67-80.
Kuttler W., Barlag A.B., Robmann F. (1996). « Study of the thermal structure of a town in a narrow valley ». Atmospheric Environment, vol. 30, n°3, p. 365-378.
Laborde J.-P., Traboulsi M. (2002). « Cartographie automatique des précipitations : application aux précipitations moyennes annuelles du Moyen Orient ». Publications de l’Association internationale de climatologie, vol. 14, p. 296-303.
Lazzarini M., Marpu P.R., Ghedira H. (2013). « Temperature-land cover interactions : the inversion of urban heat island phenomenon in desert city areas ». Remote Sensing of Environment, vol. 130, p. 136-152.
Lindberg F. (2007). « Modelling the urban climate using a local governmental geo-database ». Meteorological Applications, vol. 14, p. 263- 273.
Liu L., Zhang Y. (2011) « Urban Heat Island Analysis Using the Landsat TM Data and ASTER Data : A Case Study in Hong Kong ». Remote Sensing, vol. 3, n°7, p. 1535-1552.
Martin N. (2008). « La pollution par l’ozone et la climatologie dans un espace méditerranéen : les Alpes-Maritimes ». Thèse de doctorat, Université de Nice-Sophia Antipolis, 281 p.
Matsunaga T. (1996). « Water Surface Temperature Estimation Using Linear Equations of Brightness Temperature Observed by Advanced Spaceborne Thermal Emission and Reflection Radiometer/Thermal Infrared Radiometer (ASTER TIR) ». Journal of the Remote Sensing Society of Japan, vol. 16, n°5 p. 404-415.
Miller A.J. (2002). Subset selection in regression. Second edition. Boca Raton : Chapman and Hall/CRC, 234 p.
Obled C. (1987). « Introduction au krigeage à l’usage des hydrologues ». In Deuxièmes Journées Hydrologiques de l’ORSTOM, Montpellier : Éd. ORSTOM, p. 174-222.
Oke T.R. et al. (1991). « Simulation of surface Urban Heat Island ». Boundary-Layer Meteorology, vol. 56, n°4, p. 339-358.
Oke T.R. (1981). « Canyon geometry and the nocturnal urban heat island : comparison of scale model and field observations ». International Journal of Climatology, vol. 1, n°3, p. 237-254.
Oke T.R. (1988). « Street design and urban canopy layer climate ». Energy and Buildings, vol. 11, n°1-3, p. 103-113.
Palm R. (2002). « Utilisation du bootstrap pour les problèmes statistiques liés à l’estimation des paramètres ». Biotechnology, Agronomy, Society and Environment, vol. 6, n°3, p. 143-153.
Pielke R.A. et al. (1987). « Mesoscale numerical modelling of pollutant transport in complex terrain ». Boundary-Layer Meteorology, vol. 41, n°1-4, p. 59-74.
Rasul A., Balzter H., Smith C. (2015). « Spatial variation of the daytime Surface Urban Cool Island during the dry season in Erbil, Iraqi Kurdistan, from Landsat 8 ». Urban Climate, vol. 14, p. 176-186.
Schmid H.P. (2002). « Footprint modeling for vegetation atmosphere exchange studies : a review and perspective ». Agricultural and Forest Meteorology, vol. 113, n°1-4, p. 159-183.
Schmid H.P. (1994). « Source areas for scalars and scalar fluxes ». Boundary-Layer Meteorology, vol. 67, n°3, p. 293-318.
Segal M., Pielke R.A. (1981). « Numerical model simulation of biometeorological heat load conditions-summer day case study of the Chesapeake-bay area ». Journal of Applied Meteorology, vol. 20, n°7, p. 735-749.
Song B., Park K., (2014). « Validation of ASTER Surface Temperature Data with In Situ Measurements to Evaluate Heat Islands in Complex Urban Areas ». Hindawi Publishing Corporation Advances in Meteorology, vol. 2014, 12 p.
Vinet J. (2000). « Contribution à la modélisation thermo-aéraulique du microclimat urbain. Caractérisation de l’impact de l’eau et de la végétation sur les conditions de confort en espaces extérieurs ». Thèse de doctorat de l’Université de Nantes, 245 p.
Willmott C.J., Matsuura K. (1995). « Smart interpolation of annually averaged air temperature in the United States ». Journal of Applied Meteorology, vol. 34, p. 2577-2586.
Xian G.Z. (2015). « Remote Sensing Applications for the Urban Environment ». CRC Press, 220 p. ISBN 9781420089844
Notes
| 1. | ⇧ | Terres salées. |