La représentation cartographique des interactions spatiales ne présente pas de difficultés particulières, lorsque le nombre de lieux concernés n’excède pas la dizaine. Dans le cas contraire, la figure est caractérisée par une complexité graphique caractéristique de la représentation des données relationnelles massives (« big data ») : l’effet spaghetti.

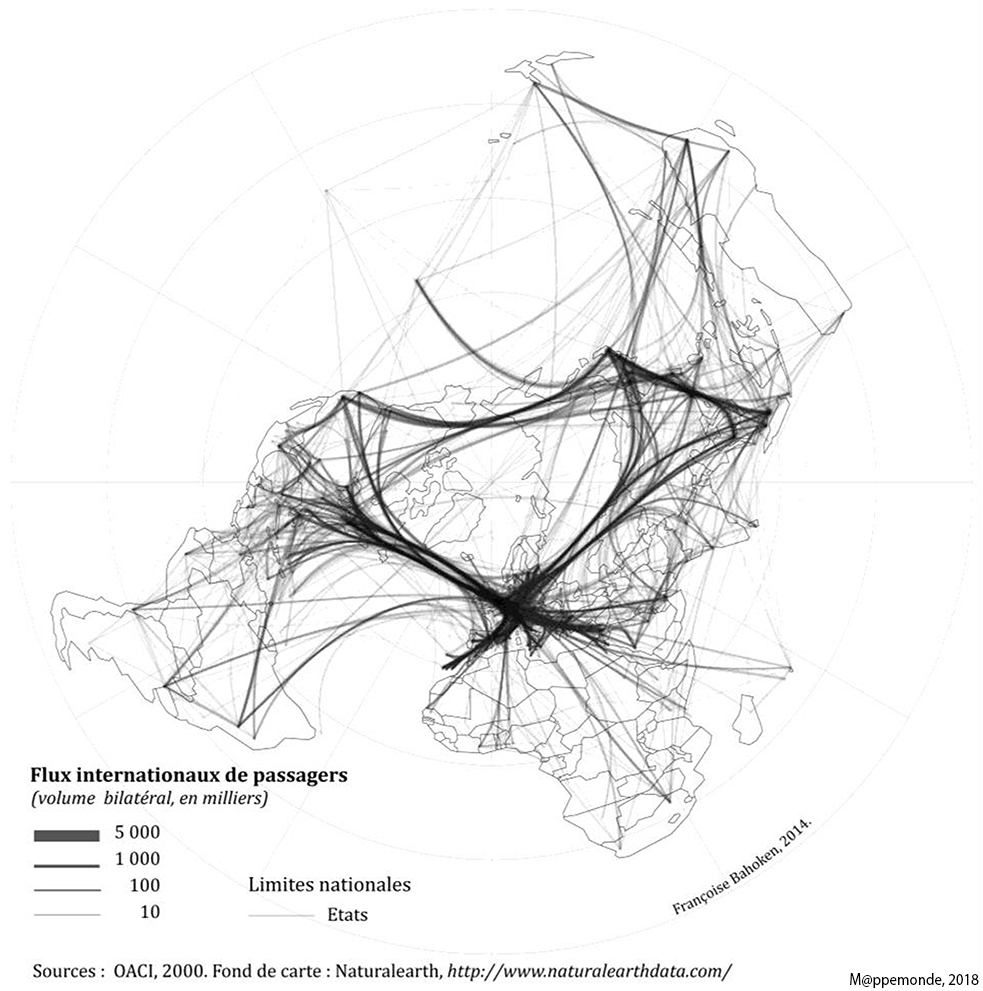
La thèse montre que deux orientations méthodologiques sont traditionnellement privilégiées pour réduire cette complexité : une sélection a priori de l’information à représenter et une réduction de la résolution des données lors de procédures d’agrégations variées. Ces possibilités sont fondées sur un raisonnement mené en amont de l’étape de représentation, lors de la modélisation de l’information statistique et/ou géographique. Si elles sont efficaces, leur principal écueil est d’entraîner la suppression de tout ou partie de l’information disponible. Pour y remédier, de nouvelles possibilités issues du champ de l’Informatique graphique sont apparues. Elles permettent notamment d’agir au niveau graphique du tracé des figurés. Les procédures de fusion des liens, une forme d’agrégation graphique, permettent, par exemple, de réduire la complexité visuelle de la carte de flux, en simulant des routes (figure 1).

Figure 1. Flux internationaux de passagers par voie aérienne (2000).

Si ces approches graphiques sont efficaces, elles ne s’appliquent pas (encore) efficacement à tous les types de flux, générant alors des cartes erronées, comme dans le cas des flux maritimes. L’une des explications de l’inadéquation de la carte de flux à la représentation de certains échanges tient au fait qu’elles sont élaborées sans considérer l’espace des flux. Dit autrement, l’espace (géographique, cognitif, etc.) n’est pas pris en compte dans le processus de représentation de flux, si ce n’est sous la forme d’habillage ou de variable lors de la modélisation numérique. C’est d’ailleurs la raison pour laquelle la solution qui consiste à visualiser des flux sous la forme de graphe – plutôt que de carte (de flux) – est pertinente.

Plus généralement, la thèse montre que les réponses classiquement apportées à la résolution des problèmes liés à l’effet-spaghetti ne s’inscrivent pas, dans l’ensemble, dans un raisonnement qui intéresse le processus de construction cartographique du flux ; elles ne s’intéressent pas à la manière dont le figuré qui symbolise le flux est perçu ou tracé. Cela signifie que les solutions [de cartographie de flux] existantes sont mises en œuvre en dehors du processus de représentation.

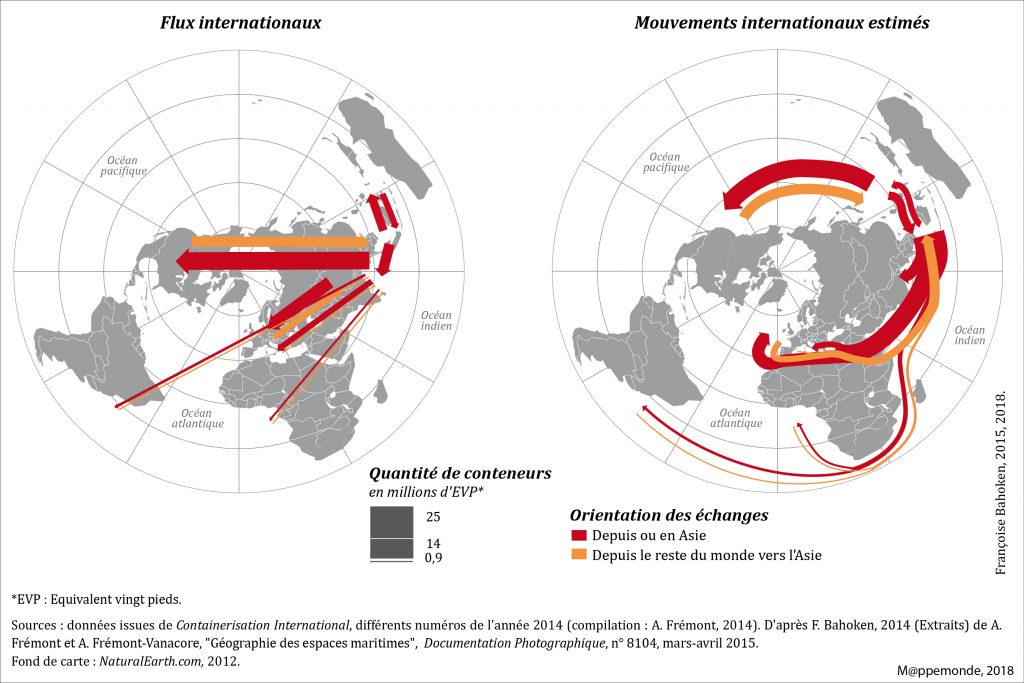
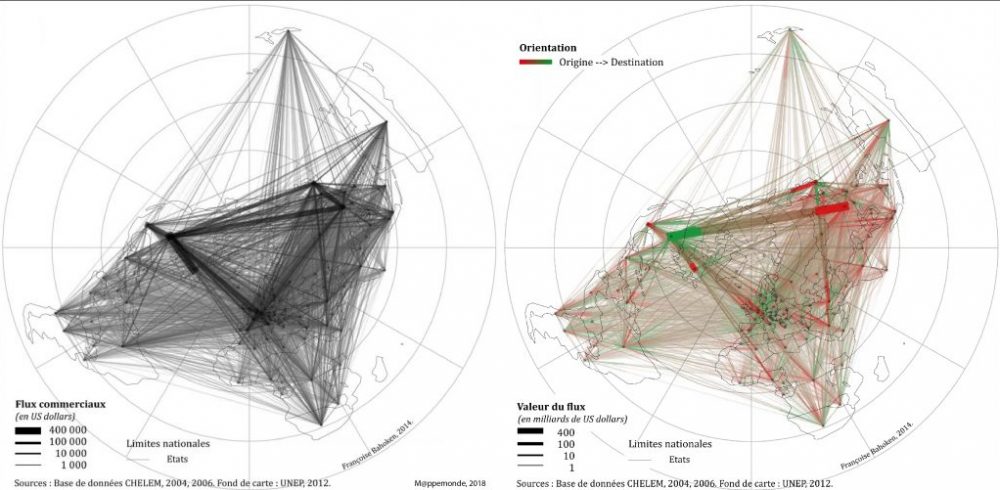
Pour y remédier, la thèse formule l’hypothèse générale que les solutions aux problèmes de complexité de la cartographie de flux intéressent également les aspects théoriques et conceptuels sous-jacents de même que des aspects cartographiques, sémiologiques et sémantiques portant sur la signification du figuré symbolisant le flux, aux côtés de questions plus classiques liées à la définition des critères de sélection. Ainsi, en examinant le processus de construction cartographique du flux, la thèse introduit la notion de mouvement. Elle établit sa signification au regard de celle de flux, dans le contexte de l’analyse des interactions spatiales. Elle démontre aussi, d’une part, l’invariance¹ du processus de construction cartographique du flux et du mouvement, quelle que soit l’échelle géographique (locale, régionale, globale), le niveau et la thématique dont il est question (flux de personnes, de marchandises, financiers…) ; d’autre part, leurs différences sémantiques (figure 2). L’impératif de cartographie des routes maritimes des mouvements de conteneurs (à droite) empêche la représentation de flux impossibles dans la réalité (à gauche) soit de navires franchissant des continents. Elle conduit à la perception d’une approximation des mouvements bilatéraux de marchandises tenant compte de l’alternance terres-mers, de la géographie.

Figure 2. Variation de la perception des quantités échangées à l’échelle mondiale.

Cette proposition essentiellement graphique est réalisée sur une matrice de flux filtrée des seuls échanges impliquant l’Asie du Sud-est. La problématique de la sélection étant cruciale, la thèse discute par ailleurs différentes manières non présentées ici de sélectionner les flux au préalable de leur représentation.

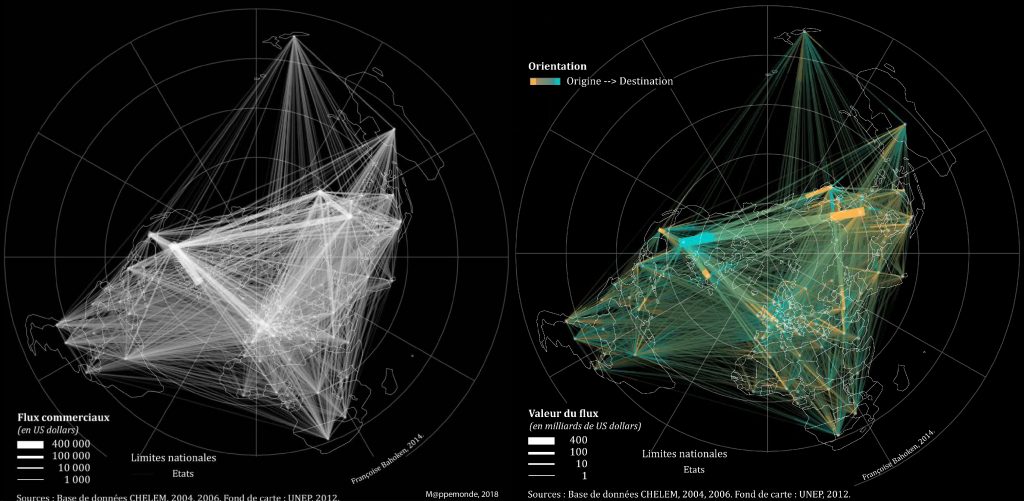
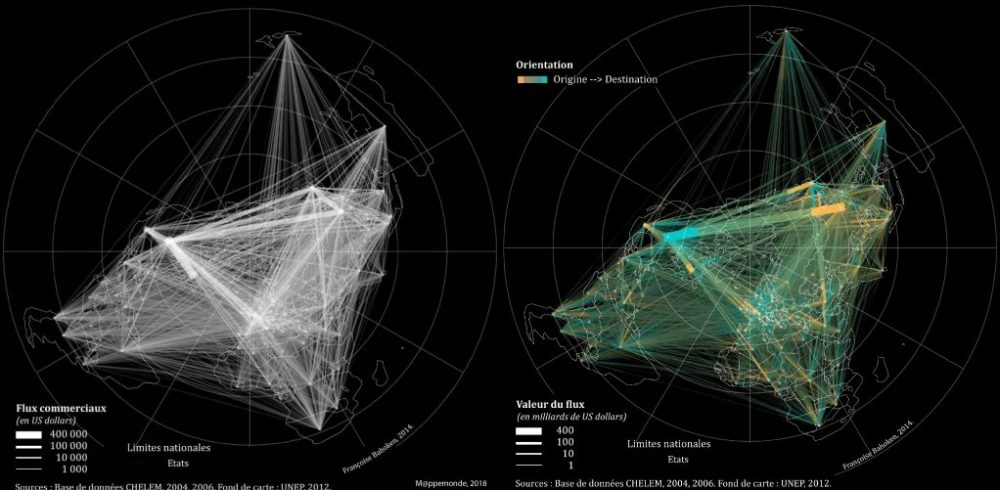
La thèse montre également qu’il est possible de cartographier des flux issus de matrices denses sans les sélectionner, en agissant sur les seuls aspects sémiologiques. Elle propose un renouvellement de l’usage de la variable visuelle (v.v.) Couleur validé empiriquement sur une matrice de flux (F) mondiaux de marchandises. Pour les représenter, il convient de décomposer la matrice correspondante en deux parties (Tobler, 1979) : l’une décrivant des volumes bilatéraux (F+) et l’autre des transferts nets ou soldes bilatéraux (F-).

La construction de (F+) consiste à tracer les flux correspondants en noir sur fond blanc, sous la forme de traits droits reliant les origines et destinations. Il s’agit aussi de mobiliser la v.v. Taille (Bertin, 1967) pour faire varier la largeur des figurés proportionnellement à leur valeur ; leur longueur étant fixée par la projection cartographique. La v.v. Transparence (Mac Eachren, 1995), nouvelle propriété morphologique formalisée par (Roth et al., 2010) pour le design de la Couleur est ensuite appliquée, dans l’objectif de faciliter la perception des motifs complexes (liée à la superposition des figurés). La carte est enfin inscrite dans la nouvelle esthétique du blanc et noir, entraînant l’inversion de la teinte du fond et des figurés. Les avantages obtenus sont multiples. Sur le plan sémiologique, les bandes étant blanches, il est possible de mobiliser d’autres informations et nuancer leur teinte pour enrichir la carte. Au niveau méthodologique, la possibilité de représenter toute l’information disponible dans la matrice sans opérer de sélection des valeurs est désormais ouverte.

Figures 3a et 3b. Flux commerciaux internationaux de marchandises

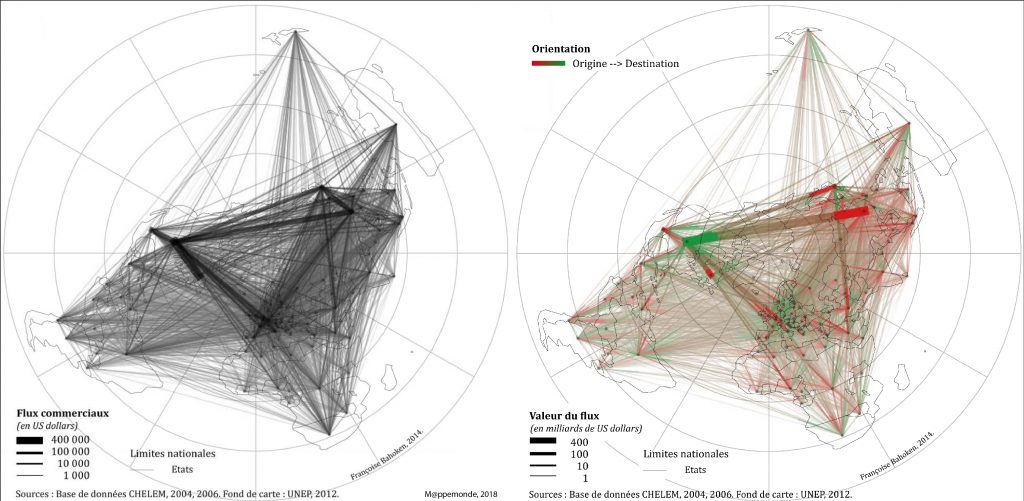
La construction de (F-) est similaire à celle de (F+). Les bandes étant blanches et plus ou moins translucides, il leur est appliqué le principe d’opposition colorée de teinte spécifique à la v.v. Couleur, à la manière des aplats de teintes divergentes autour d’une référence. Le transfert de ce principe est théoriquement possible puisque les matrices de flux antisymétriques sont caractérisées par des valeurs identiques de part et d’autre de la diagonale principale – c’est pour cela qu’on mobilise une bande –, mais sont de signes opposés, ce qui justifie le recours à l’opposition colorée. Sur le plan sémiologique, par exemple, il n’est désormais plus nécessaire de réaliser deux cartes pour représenter des transferts nets, une seule suffit pour combiner les importations et les exportations.

Il est intéressant que noter que ces cartes, pourtant réalisées sans traitement des données numériques, vont se révéler fondamentales au niveau théorique et conceptuel. Leur sémiologie entraîne en effet l’émergence d’un effet de profondeur non mis en évidence jusque-là. En révélant différentes classes de longueurs de liens, ces cartes suggèrent l’hypothèse d’un emboitement d’échelles spatiales dans l’expression de ces mobilités. Elles interpellent la notion de distance parcourue par le flux… que l’on représente justement sur une carte par la longueur du lien, alors que seule leur largeur est mobilisée ici. Elles interpellent l’échelle géographique, plus largement le système de projection cartographique. Elles soulèvent in fine le caractère essentiel du questionnement devant d’ailleurs précéder le choix du critère de sélection des flux (ou des mouvements) à cartographier à savoir : est-il plus important de représenter 4 000 personnes qui se déplacent sur 10 km ou bien 40 personnes qui se déplacent sur 1 000 km ?

Références

Bertin J. (1967). « La représentation du mouvement dans le plan ». In Bertin J., Sémiologie graphique, Paris : Gauthier-Villars, p. 342-355.

Mac Eachren A. (1995). How maps work. New York : The Guilford Press, 513 p. ISBN 9780898625899

Roth R.E., Woodruff A.W., Johnson Z.F. (2010). « Value-by-alpha Maps : An alternative technique to the cartogram ». The Cartographic Journal, vol. 47, n°2, 12 p.

Tobler W. R. (1979). « Estimations of attractivities from interactions ». Environment and Planning A, vol. 11, n°2, p. 121-127.

Références de la thèse

Bahoken F. (2016). Contribution à la cartographie d’une matrice de flux. Thèse de doctorat, Université Paris Diderot (Paris 7), Sorbonne Paris Cité, 408 p. +Ann.